Od doby, kdy někdo prohlásil, že čmelák ani včela nemohou létat, rádi říkáme, že to dotyčný hmyz určitě neví, a proto létá. Nyní nastal čas, abychom řekli včelkám a čmelákům: Už můžete létat.
Klasická aerodynamika let čmeláka nevysvětlí
Domněnka o nemožnosti letu čmeláka a včely pramení z toho, že kdosi použil aerodynamiku, která se osvědčila u všech současných letadel a vrtulníků, na malý hmyz. Je to něco podobného, jako byste šli s klasickou fyzikou na kvantové jevy – vycházely by úplné nesmysly. Jak jsme na začátku dvacátého století objevovali kvantovou mechaniku, tak teprve nyní pronikáme do záhad letu hmyzu. Dnes umíme zjistit chování letadel s komplikovaným tvarem křídla při různých rychlostech a úhlech náběhu. Výpočty dobře souhlasí s praxí. Co se stane, když totéž použijeme pro křídla včely? Proč to nefunguje? Teorie aplikované na velká letadla pracují zejména se statickým obtékáním profilu křídla. Nabíhající proud vzduchu má konstantní rychlost a nanejvýš zahrnujeme změnu úhlu náběhu v jednotkách stupňů. Ale obyčejná včela mávne křidélky asi dvěstěkrát za sekundu. Dokážete si jistě představit, jaké vzdušné víry, i když miniaturní, vznikají. A to je důvod, proč klasická aerodynamika selhává a zároveň v tom spočívá kouzlo čmeláčího letu.
Tři kouzla udrží čmeláka ve vzduchu
Teprve na konci dvacátého století jsme začali pomalu pronikat do tajů hmyzího letu. Objevili jsme tři základní druhy vzniku vztlaku, které běžné teorie nezahrnují, ale pro včely a čmeláky jsou klíčové. Tyto tři jevy popisují síly vznikající za letu hmyzu s velmi malými odchylkami.
Nedříve vědci přišli na to, že hmyzí křídla nejsou obtékána laminárně ani turbulentně, nýbrž převážně vírově. Vírové proudění bylo poprvé popsáno až začátkem devadesátých let. Narozdíl od laminárního a turbulentního proudění zde nesledují proudnice ani přibližně tvar obtékaného profilu, ale na podtlakové (v běžné poloze horní) části se vytvoří vír. To nastane při velkém úhlu náběhu křídla vůči vzduchu. Při vírovém proudění je vztlak výrazně vyšší než u jiných druhů, ale dopředný odpor je také velký, tudíž křídla velkých letadel takto obtékaná nikdy nebudou.
Později výzkumníci objevili, že pouhé vírové proudění by stále včelu/čmeláka neuneslo a vypočtené hodnoty vztlaku se stále neshodovali s experimentálními naměřenými na modelu mávajících muších křídel. Pátrali dále a přišli na to, že se křidélka při rychlém pohybu nahoru a dolů dostávají do oblasti, kde je vzduch rozvířen od předchozího mávnutí – takzvaného úplavu. Když to zahrnuli do výpočtů, výrazně se přiblížili naměřeným hodnotám. Včely už skoro mohly létat. Scházelo vysvětlit maxima sil v horní a dolní poloze křídel, kde rychlost mávání mění směr.
Tento jev je asi nejsložitější. Je způsoben tím, že včelka, čmelák nebo jakýkoliv “hmyzák” v horní a dolní “úvrati” natáčí křídlo kolem jeho nejdelší osy o poměrně velký úhel. Potom u křídla nastane obdoba Magnusova efektu, který například způsobuje falše u vhodně nakopnutých fotbalových míčů či správně odehraných ping-pongových míčků. Na jedné straně rotujícího tělesa je rychlost pohybu vůči okolí vyšší než na druhé a to způsobí rozdíl tlaků na protilehlých stranách , a tím zatáčení ve směru kolmém na osu rotace. Válec rovnoběžný se zemí roztočený na velké otáčky (Flettnerův rotor) s nějakou počáteční dopřednou rychlostí by mohl nést i letadlo místo křídla. Takové pokusy probíhaly jak na letadlech, tak na lodích (válec umístěný svisle místo plachet). Mezi kulatým tvarem válce či koule a plochým hmyzím křídlem je zásadní rozdíl, ale princip vzniku síly je obdobný.
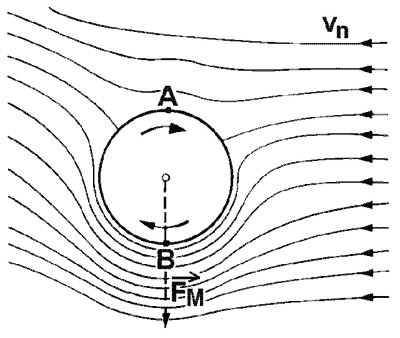
Credit: Ruprecht Nennstiel
Po odhalení těchto tří jevů, jsme schopni vysvětlit let malého hmyzu s rychle mávajícími křídly. Vážky se dvěmi páry velkých křídel jsou něco jiného, i když výše uvedené se u nich projevuje také.
Jak létá včela
Nedávno se vědci zaměřili přímo na let včely. Natáčeli její let kamerou rychlostí 2 tisíce snímků za sekundu. Záběry poté analyzovali a zjistili, že včela mává křídly v rozpětí pouhých 90° s frekvencí přibližně 230 mávnutí za sekundu. Mouchy a podobný hmyz mává v rozpětí přesahujícím 100°, někdy se přiblíží 180° s frekvencí v závislostí na velikosti. Čím menší “muška”, tím rychleji mává. Moskyt zvládne v jedné sekundě 400 mávnutí. Vzhledem ke své velikosti mává včelka velmi rychle. Osmdesátkrát lehčí pestřenka v jedné sekundě stihne o 30 kmitů méně.
Co se stane, když včelka nabere zásobu nektaru a pylu a stane se skoro dvakrát těžší? Na první pohled by se zdálo, že začne křídly kmitat rychleji. Pravdou je, že pouze zvětší oblouk, ve kterém křidélky mává. Energeticky efektivnější by při tom skutečně bylo zvýšení frekvence. To však včelka neumí, protože ji v tom brání konstrukce svalů, která je přizpůsobena kmitaní na 230 Hz. Ostatně právě svaly mají včely odlišné od jiných druhů hmyzu, takže si létají po svém.
Robotická včela
Cílem výzkumu je poznat plně aerodynamiku a mechaniku letu hmyzu nejen z čisté zvědavosti, ale zvláště proto, abychom mohli v budoucnu vyrobit létajícího mikrorobota – robotickou včelu nebo mouchu. Ty by sice mohly sloužit pro zábavu, vybavené kamerou k vyhledávání lidí v nepřístupných prostorách nebo také pravděpodobněji k vojenským účelům. Malá dálkově ovládaná muška s kamerou a mikrofonem je ideální pro odposlech a špionáž. Velmi nepříjemné by bylo, kdyby místo kamery nesla chemické nebo biologické zbraně. Několik much by snadno zlikvidovalo přesně vybrané oběti.
Ať už se z robotického hmyzu vyvine cokoliv, už nikdo nemůže říct, že by čmelák nebo včela neměla létat. Už víme, že létat mohou a žádná teorie jim v tom nebrání.
Další informace
- Wing Rotation and the Aerodynamic Basis of Insect Fligh (18. 6. 1999) – Rotace křídla a základy aerodynamiky letu hmyzu. Článek je přístupný po registraci zdarma.
- Unsteady aerodynamic performance of model wings at low Reynolds numbers (pdf 239 kB) (17. 8.1992) – Nestabilně aerodynamická výkonnost modelů křídel při nízkých Reynoldsových číslech
- Measuring wing kinematics, flight trajectory and body attitude during forward flight and turning maneuvers in dragonflies (29. 11. 2002) – Měření kinematiky křídel, trajektorie letu a tělesných poměru během dopředného letu a otáčení vážek
- The Flight of the Bumblebee – Let čmeláka – stručné shrnutí vývoje kolem “záhady” letu čmeláka
- Scientists Finally Figure Out How Bees Fly (9. 1.2005) – Jeden z mnoha článků, který ohlašuje vyřešení “záhady” letu včely
- Dickinson Lab – Laboratoř snažící se vyrobit robotický hmyz
Jirka Cech – WWW – 23.1.2006
Martin – WWW – 23.1.2006
Renata Křížová – WWW – 17.2.2006
Pavlik – 10.4.2006
Vilda – 8.11.2007
Radek – 29.7.2010
Václav – WWW – 21.8.2012